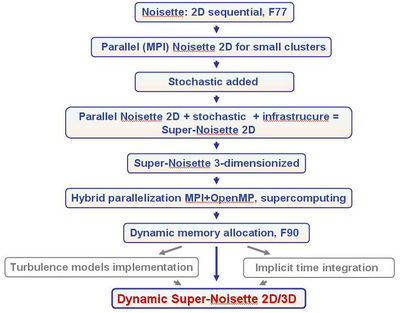
The parallel in-house research CFD CAA code NOISETTE
|
 |
 |
Institute for Mathematical Modelling (IMM) of Russian Academy of Science (RAS)
|
- Explicit high-order algorithms for unstructured 2D (triangular) and 3D (tetrahedral) meshes
- DNS of compressible viscous flows and aeroacoustics (DNC, NLDE)
- High efficiency on thousands of CPUs of a supercomputer even for small meshes
- Hybrid MPI+OpenMP parallelization
- Language: computational part - Fortran 90, infrastructure - C++
|
Authors: I. Abalakin, A. Gorobets, T. Kozubskaya, D. Kolmogorov, A. Duben, I. Borovskaya
Original sequential 2D version designed in IMM RAS together with INRIA, Sophia-Antipolis, France
(Abalakin I. V., Kozubskaya T. K., A. Dervieux, C. Debiez)
|
Mathematical basis
- Euler Equations (EE)
- Navier-Stokes Equations (NSE)
- Nonlinear Disturbances Equations (NLDE)
- Linearized Euler Equations (LEE)
- Linearized Navier-Stokes Equations (NSE)
|
Numerical Techniques Implemented
Space Approximation
Multi-parameter vertex-centered scheme (up to 6th order)
Time Integration
Runge-Kutta method, Low-storage Runge-Kutta method (up to 4th order)
Linear Low-storage Runge-Kutta method (arbitrarily high order)
Boundary Conditions
Steger-Warming flux splitting based inflow and outflow BC
Characteristic BC
Non-reflecting (radiation and outflow, buffer zones)
Non-local transparent BC
|
Parallel performance
|
|
Parallel algorithm is based on a hybrid MPI+OpenMP approach which better fits modern architecture of a supercomputer with multi-core nodes.
Following figures demonstrate high parallel efficiency even for a small problem.
The high order scheme with the large space stencil is used in the tests.
|
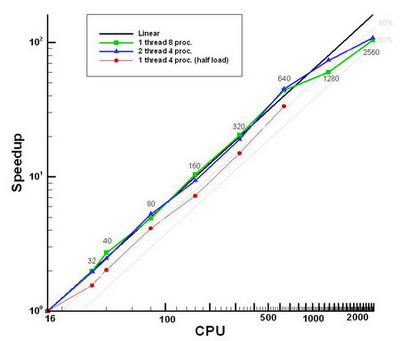
Supercomputer MVS 100000 (JSC RAS)
Mesh size is only ~106 nodes
 |
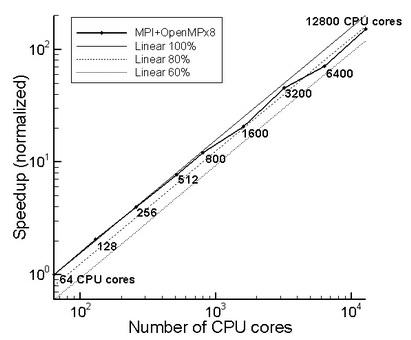
Supercomputer Lomonosov (MSU)
Mesh size 1.6*107 nodes
 |
Current applications
- Numerical experiments on acoustic liners (Jet engine noise reduction devices)
- Optimization of acoustic sensors for mobile robots
- Modeling of impedance tubes with resonator chambers
- Complex flows around obstacles considering acoustic effects
Development directions
- General object-oriented restructuring of the code (Gorobets, Kozubskaya)
- Implementation of turbulence models RANS, DES, LES (Abalakin, Kolmogorov)
- Implicit time integration algorithm (Abalakin, Kolmogorov)
- Parallel algorithm improvements (Gorobets)
- New types of boundary conditions - periodic BC, non-local BC, etc.
- Infrastructure extension
|
|
Publications:
- A.V.Gorobets, T.K.Kozubskaya, “Technology of parallelization of the explicit high-accuracy algorithms for CFD and CAA on non-structured meshes”, Mathematical modeling, vol. 19, number 2, pp. 68-86, 2007
- A.V. Gorobets, I.V. Abalakin, T.K. Kozubskaya, “Technology of parallelization for 2D and 3D CFD/CAA codes based on high-accuracy explicit methods on unstructured meshes”, Parallel CFD 2007, Antalya (Turkey), May 2007
- Abalakin I.V., Dervieux A., Kozubskaya T.K. "High Accuracy Finite Volume Method for Solving
Nonlinear Aeroacoustics Problems on Unstructured Meshes", Chinese Journal of Aeronautics,
Vol. 19, No 2, 2006.
- Tatiana K. Kozubskaya, "Validation and Verification in Computational Aeroacoustics:
from Linear to Nonlinear" - In A series of Handbooks on Theory and Engineering Applications of Computational Methods. Verification and Validation Methods for Challenging Multiphysics Problems, CIMNE, Barcelona (2006), pp. 187-208
|
|