KSFD algorithm for Poisson equation with one periodic direction
|
|
Authors: A. Gorobets, F. X. Trias, M. Soria
|
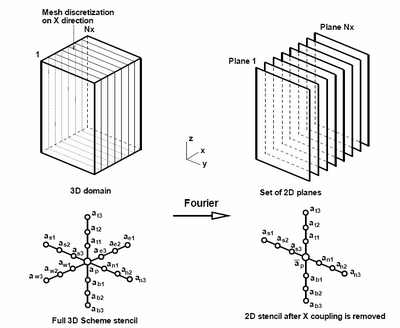
The Krylov-Schur-Fourier Decomposition algorithm (KSFD) is based on a combination of Fourier
decomposition which uncouples 3D problem into set of 2D problems (planes). The 2D problems are solved
with the Preconditioned Conjugate Gradient (PCG) Krylov subspace iterative method
and the Direct Schur Decomposition (DSD) direct method.
| 
|
Algorithm
- Fourier diagonalization using FFT uncouples 3D problem into set of independent 2D problems (planes)
- DSD and PCG methods are used to solve the 2D problems that corresponds to lower and higher Fourier frequencies respectively
- Inverse FFT restores the solution of the 3D problem
|
Basic features
- The implementation of the Direct Schur method requires a time-consuming preprocessing but needs only
one communication of reduction type to obtain solution.
- Performs well on both small "Beowulf" clusters and supercomputers
- The problem to solve must have (at least) one periodic direction, mesh step must be uniform in this direction
- The geometry of 3D obstacles is limited to be a 2D shape extruded along the periodic direction
|
Performance demonstration
|
Speedup for a small problem
Mesh size 1.7*106(mesh1) and 1.1*107, 4-th order discretization, differentially heated cavity (DHC) case.
The figure demonstrates how the KSFD solver adapts to different CPU numbers
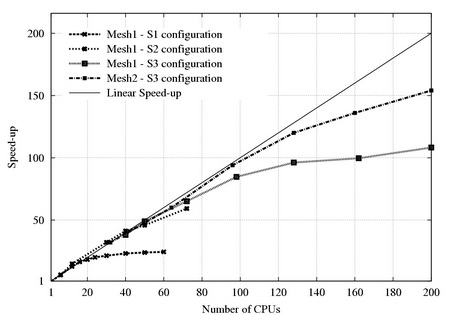Different delimiter choice: S1 - D=32 (direct method, all planes are solved with DSD); S2 - D=5 (the first 5 planes with DSD), S3 - D=1 (only the first plane with DSD)
|
Speedup for big DNS cases, Lomonosov supercomputer
Mesh size 3.3*108 (left) and 109 (right), differentially heated cavity (DHC) case.
|
Scalability demonstration
|
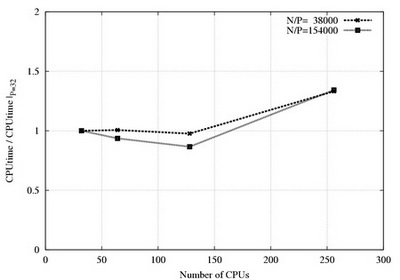
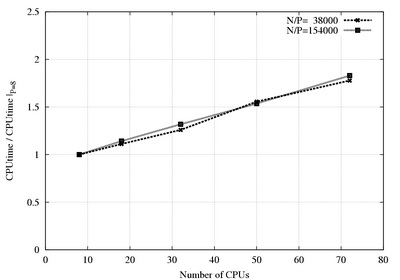
The "weak" speedup is shown on the following figures. The problem size per CPU is constant when CPU number vary.
Mesh size per CPU is 38000 (dotted) and 154000 (solid), 4-th order discretization, differentially heated cavity (DHC) case.
|
Scalability in the periodic direction
|
Scalability in the two non-periodic directions
|
Reference
- A. Gorobets, F. X. Trias, M. Soria and A. Oliva, “A scalable parallel Poisson solver for three-dimensional
problems with one periodic direction”, Computers & Fluids journal, 39 (2010) 525-538, Elsevier
-
A.V.Gorobets, “Scalable algorithm for incompressible flow simulation on parallel computer systems”, Mathematical modeling, vol. 19, number 10, pp. 105-128, 2007
- F. X. Trias, A.V. Gorobets, M. Soria and A. Oliva, "DNS of natural convection flows on MareNostrum supercomputer", Parallel CFD 2007, Antalya (Turkey), May 2007
| |